Hello World 👋
In this article, we will see how bit manipulation could be a real lifesaver for competitive coding as well as for a technical interview.
So what is Bit manipulation?
Bit manipulation is the act of algorithmically manipulating bits or other pieces of data shorter than a word. This is the process of performing logical operations on bit sequences in order to reach the desired result. Bit manipulation allows us to use these operators to reach certain sequences in a clean and efficient manner, which is just one reason why it’s essential to understand what operators are available and how we can make use of them.
Bit manipulation, in some cases, can obviate or reduce the need to loop over a data structure and can give many-fold speedups, as bit manipulations are processed in parallel, but the code can become more difficult to write and maintain.
At the heart of bit manipulation are the bit-wise operators & (and), | (or), ~ (not) and ^ (exclusive-or, xor) and shift operators a << b and a >> b.
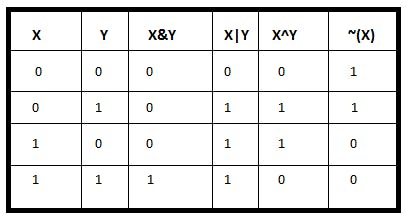
Refer this for Understanding how these operators work.
Okay So What Next?
Now we will take examples one by one where bit manipulation can be used.
1. Count the Number of 1's in Binary Representation of a Number
int count_one(int n) {
while(n) {
n = n&(n-1);
count++;
}
return count;
}
2. Sum of two Integer Adding two numbers without using the + operator.
Use ^ and & to add two integers
int getSum(int a, int b) {
return b==0? a:getSum(a^b, (a&b)<<1); //be careful about the terminating condition;
}
3. Missing Number: Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one that is missing from the array.
For example, Given nums = [0, 1, 3] return 2.
int missingNumber(vector<int>& nums) {
int ret = 0;
for(int i = 0; i < nums.size(); ++i) {
ret ^= i;
ret ^= nums[i];
}
return ret^=nums.size();
}
4. Largest power of Two: Find the largest power of 2 (most significant bit in binary form), which is less than or equal to the given number N.
long largest_power(long N) {
//changing all right side bits to 1.
N = N | (N>>1);
N = N | (N>>2);
N = N | (N>>4);
N = N | (N>>8);
N = N | (N>>16);
return (N+1)>>1;
}
5. Reverse Bits: Reverse bits of a given 32 bits unsigned integer.
uint32_t reverseBits(uint32_t n) {
unsigned int mask = 1<<31, res = 0;
for(int i = 0; i < 32; ++i) {
if(n & 1) res |= mask;
mask >>= 1;
n >>= 1;
}
return res;
}
uint32_t reverseBits(uint32_t n) {
uint32_t mask = 1, ret = 0;
for(int i = 0; i < 32; ++i){
ret <<= 1;
if(mask & n) ret |= 1;
mask <<= 1;
}
return ret;
}
6. Bitwise & of Number Range Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive.
For example, given the range [5, 7], you should return 4.
int rangeBitwiseAnd(int m, int n) {
int a = 0;
while(m != n) {
m >>= 1;
n >>= 1;
a++;
}
return m<<a;
}
7. Number of '1' Bits Write a function that takes an unsigned integer and returns the number of ’1' bits it has (also known as the Hamming weight ).
int hammingWeight(uint32_t n) {
int count = 0;
while(n) {
n = n&(n-1);
count++;
}
return count;
}
int hammingWeight(uint32_t n) {
ulong mask = 1;
int count = 0;
for(int i = 0; i < 32; ++i){ //31 will not do, delicate;
if(mask & n) count++;
mask <<= 1;
}
return count;
}
8.Majority Element Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times. (bit-counting as a usual way, but here we actually also can adopt sorting and Moore Voting Algorithm)
int majorityElement(vector<int>& nums) {
int len = sizeof(int)*8, size = nums.size();
int count = 0, mask = 1, ret = 0;
for(int i = 0; i < len; ++i) {
count = 0;
for(int j = 0; j < size; ++j)
if(mask & nums[j]) count++;
if(count > size/2) ret |= mask;
mask <<= 1;
}
return ret;
}
9. Single Number Given an array of integers, every element appears three times except for one. Find that single one. (Still, this type can be solved by bit-counting easily.) But we are going to solve it by a digital logic design.
//inspired by logical circuit design and boolean algebra;
//counter - unit of 3;
//current incoming next
//a b c a b
//0 0 0 0 0
//0 1 0 0 1
//1 0 0 1 0
//0 0 1 0 1
//0 1 1 1 0
//1 0 1 0 0
//a = a&~b&~c + ~a&b&c;
//b = ~a&b&~c + ~a&~b&c;
//return a|b since the single number can appear once or twice;
int singleNumber(vector<int>& nums) {
int t = 0, a = 0, b = 0;
for(int i = 0; i < nums.size(); ++i) {
t = (a&~b&~nums[i]) | (~a&b&nums[i]);
b = (~a&b&~nums[i]) | (~a&~b&nums[i]);
a = t;
}
return a | b;
}
;
10. Reversing Bits in Integer:
x = ((x & 0xaaaaaaaa) >> 1) | ((x & 0x55555555) << 1);
x = ((x & 0xcccccccc) >> 2) | ((x & 0x33333333) << 2);
x = ((x & 0xf0f0f0f0) >> 4) | ((x & 0x0f0f0f0f) << 4);
x = ((x & 0xff00ff00) >> 8) | ((x & 0x00ff00ff) << 8);
x = ((x & 0xffff0000) >> 16) | ((x & 0x0000ffff) << 16);
Wrap Up
Bit Manipulation is used in many ways in different problems, practice problems on different platforms in order to master it.
#Happy_Coding 💻
Thank you for reading the article. Follow CodoPedia for More. 😃
For regular updates and more interesting stuff Join us on Telegram
