Data structures and Algorithms are always a hot topic in the computer science field, old and gold, no matter how many buzz words come in this field but data structures are the base of all the things in the IT field. Also, when it comes to placement season whether on-campus or off-campus data structures will always help you when you want to get into a well-known product based company as a Software Developer. But students are always confused about how to start it, how to practice it, and how to understand the concepts clearly in-depth and apply them in Competitive Coding. So, here we will discuss how to clear the DSA concepts and always be Interview Ready. These are the basic concepts that constitute making the code efficient by helping in designing an optimized solution. This blog will consist of a complete learning path of data structure and algorithms.

What are Data Structures?
The data structures are ways to store, organize, and manage the data and algorithms are the instructions to perform a task on these data structures and solve a well-defined problem.
From where should we study?
So there are many resources available for Data structures and Algorithms, whether they are free or paid, all of them are good but there are few topics which are best in a particular resource. Therefore, we will see the best resource for a particular topic in this blog.
Where to start from?
The first question that comes to our mind is from which data structure we should start, but that's the wrong question, the question is "Is there anything pre-requisite?", Yes there is, we should always start with time and space complexity analysis, only after studying this we will understand that why and how a particular Data structure is useful and in what way.
Time and Space Complexity
To study time and space complexity analysis you can refer Ravindra Babu lectures available on Youtube and interview bit for practice.
Now, as soon as you are clear with time and space complexity, you are ready to study each and every data structure and different algorithms using those data structures.
Check famous Cheat Sheet for different algorithms
Arrays
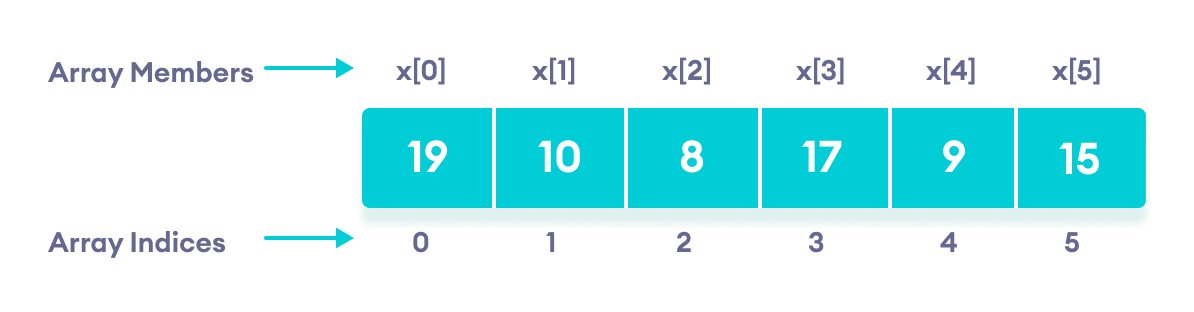
An array is a collection of items stored at contiguous memory locations. The idea is to store multiple items of the same type together.
Dynamic Arrays and How they work
A Dynamic array (vector in C++, ArrayList in Java) automatically grows when we try to make an insertion and there is no more space left for the new item. Usually, the area doubles in size.
There are multiple techniques used to array problems so it is must to go through those concept in order to master the array problems.
Linked Lists
A linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers.
Practice Linked List problems here
Stack
A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates, etc.
Basic Operations Stack operations may involve initializing the stack, using it, and then de-initializing it. Apart from these basic stuff, a stack is used for the following two primary operations.
push() − Pushing (storing) an element on the stack.
pop() − Removing (accessing) an element from the stack.
To use a stack efficiently, we need to check the status of the stack as well. For the same purpose, the following functionality is added to stacks −
peek() − get the top data element of the stack, without removing it.
isFull() − check if stack is full.
isEmpty() − check if stack is empty.
Practice Linked list questions here
Queue
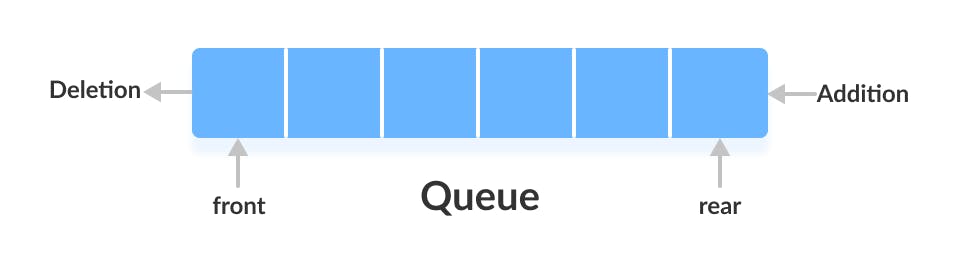
A Queue is a linear structure that follows a particular order in which the operations are performed. The order is First In First Out (FIFO).
Basic Operations Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues −
enqueue() − add (store) an item to the queue.
dequeue() − remove (access) an item from the queue.
Few more functions are required to make the above-mentioned queue operation efficient. These are −
peek() − Gets the element at the front of the queue without removing it.
isFull() − Checks if the queue is full.
isEmpty() − Checks if the queue is empty.
In a queue, we always dequeue (or access) data, pointed by the front pointer and while enqueuing (or storing) data in the queue we take help of rear pointer.
Binary Tree
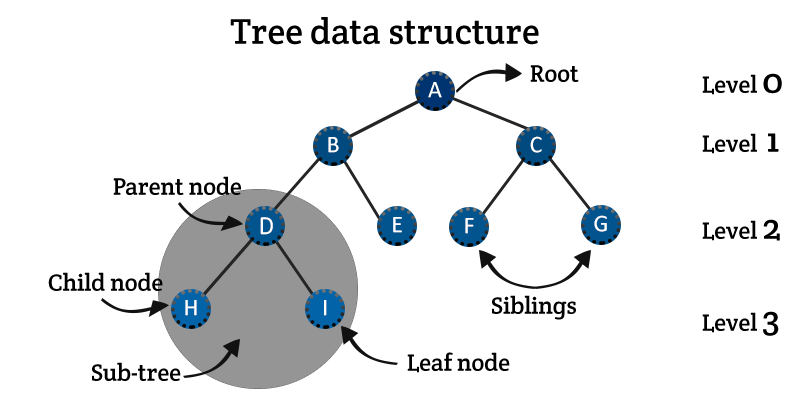
A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
Inorder Pre-order Post-order Trick
Types of Trees
1. Binary Search Trees- Notes
Binary Search Trees Video Insertion and Deletion
Binary Search Tree Practice Problems
2. AVL Trees- Notes
AVL Tree Video Insertion and Rotations
3. Red Black Trees- Notes
Red Black Tree Introduction Video
Red Black Tree Insertion Implementation
Red Black Tree Deletion Implementation
4. Splay Trees- Notes
5. Fenwick Tree- Notes
Practice Binary Tree Problems here
Heap
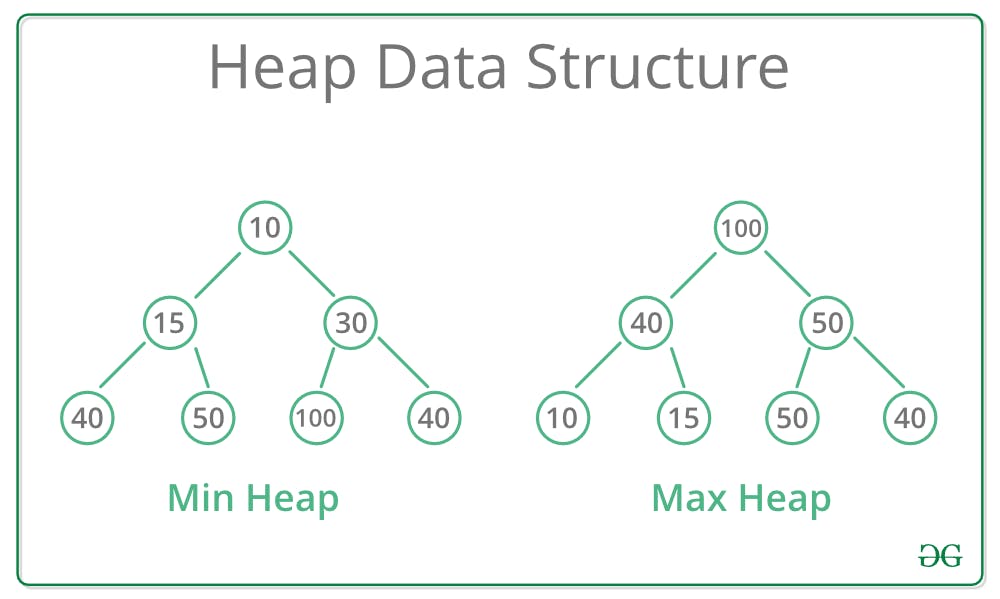
A Heap is a special Tree-based data structure in which the tree is a complete binary tree. Generally, Heaps can be of two types:
Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of its children. The same property must be recursively true for all sub-trees in that Binary Tree. Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of its children. The same property must be recursively true for all sub-trees in that Binary Tree.
Hashing
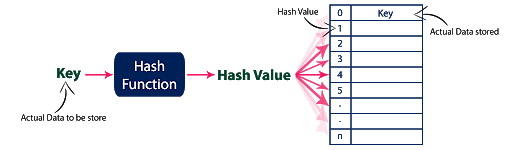
Hashing is an important Data Structure which is designed to use a special function called the Hash function which is used to map a given value with a particular key for faster access of elements. The efficiency of mapping depends of the efficiency of the hash function used.
Hashing Introduction Video-MIT
Hashing Video easy to understand and short
Graph
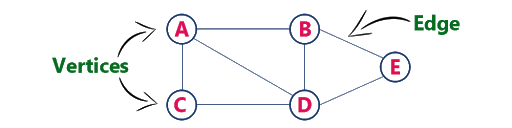
A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.
A graph is a common data structure that consists of a finite set of nodes (or vertices) and a set of edges connecting them.
A pair (x,y) is referred to as an edge, which communicates that the x vertex connects to the y vertex.
Types of graphs: Undirected Graph: In an undirected graph, nodes are connected by edges that are all bidirectional. For example if an edge connects node 1 and 2, we can traverse from node 1 to node 2, and from node 2 to 1.
Directed Graph In a directed graph, nodes are connected by directed edges – they only go in one direction. For example, if an edge connects node 1 and 2, but the arrow head points towards 2, we can only traverse from node 1 to node 2 – not in the opposite direction.
Breadth First Search and Depth First Search Video
Shortest Path Algorithms Notes
Dijkstra's shortest path algorithm
Articulation Points and Bridges
Strongly Connected Components Video
Practice Graph Algorithms Here
Dynamic Programming

Dynamic Programming (DP) is an algorithmic technique for solving an optimization problem by breaking it down into simpler subproblems and utilizing the fact that the optimal solution to the overall problem depends upon the optimal solution to its subproblems.
Dynamic Programming Introduction Notes-1
Dynamic Programming Introduction Video
Best Videos for Standard Problems
Tries
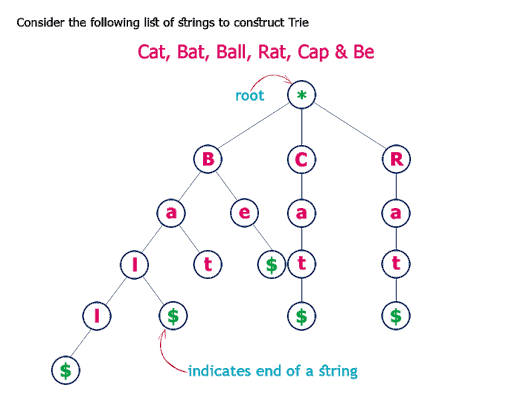
Trie is a data structure which is used to store the collection of strings and makes searching of a pattern in words more easy. The term trie came from the word retrieval. Trie data structure makes retrieval of a string from the collection of strings more easily. Trie is also called as Prefix Tree and some times Digital Tree.
Trie Code for Insert and Search
Segment Tree
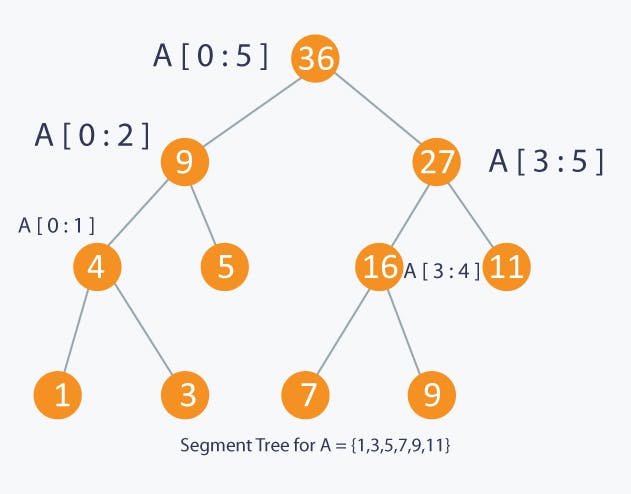
A Segment Tree is a data structure that allows answering range queries over an array effectively, while still being flexible enough to allow modifying the array. This includes finding the sum of consecutive array elements a[l…r], or finding the minimum element in a such a range in O(logn) time. Between answering such queries the Segment Tree allows modifying the array by replacing one element, or even change the elements of a whole subsegment (e.g. assigning all elements a[l…r] to any value, or adding a value to all element in the subsegment).
Segment Tree Introduction Video
Disjoint Set
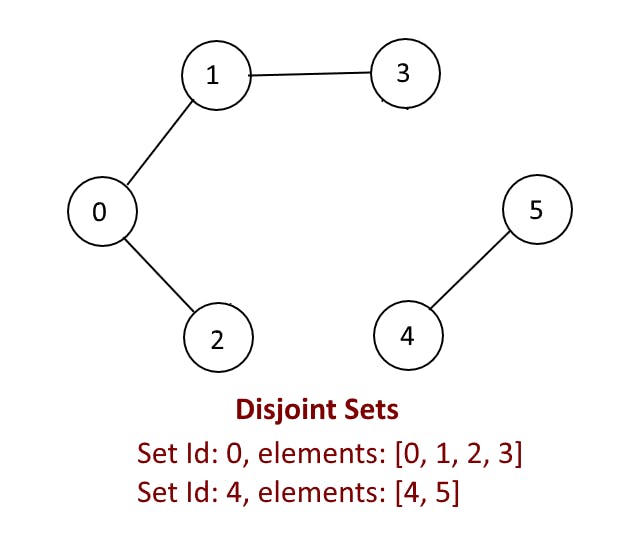
Disjoint Set Data Structure-Notes 1
Disjoint Set Data Structure-Notes 2
Wrap Up
These are the commonly used data structure and algorithms. The journey of learning algorithms never ends.
#Happy_Coding 💻
Thank you for reading the article. Follow CodoPedia for More. 😃
For regular updates and more interesting stuff join our telegram community here Telegram


